2-SAT problem and its polynomial time algorithm
1. What is 2-SAT?
2-SAT (2-Satisfiability) is a special case of the Boolean satisfiability problem. It asks whether there is a way to assign True or False to variables so that a Boolean formula is satisfied. In 2-SAT, each clause has exactly two literals.
Example:
(x1 ∨ ¬x2) ∧ (¬x1 ∨ x3) ∧ (x2 ∨ x3)
- x1, x2, x3 are Boolean variables.
- ∨ means OR, ∧ means AND, ¬ means NOT.
- Goal: assign values to make all clauses true.
- A clause is satisfied if at least one of its literals is True.
- A formula is satisfied if all clauses are satisfied.
2. Intuition for algorithm
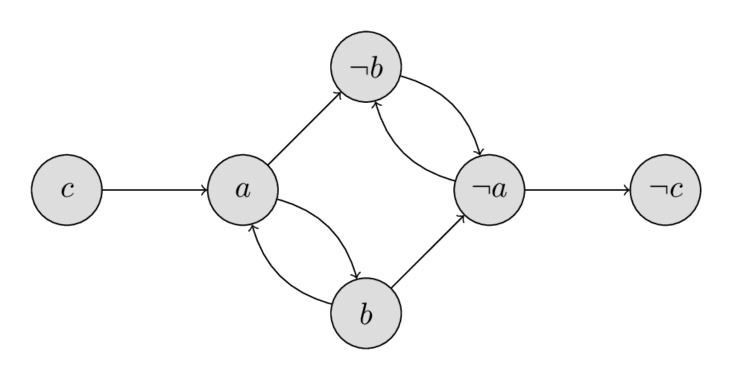
Each clause involves two variables of the form (a ∨ b).
A clause (a ∨ b) can be rewritten as:
- ¬a → b (If a is False, b must be True)
- ¬b → a (If b is False, a must be True)
Therefore can be thought as a graph theory problem where:
Nodes: all literals and their negations (a, ¬a, b, ¬b)
Edges: each implication becomes a directed edge
¬a → b
¬b → a
This graph encodes all constraints and dependencies as an edge ¬a → b shows a forced relationship: if ¬a is chosen, b must follow. By following paths along the graph, we can propagate forced assignments across variables.
3. Algorithm to solve 2-SAT
- Construct Implication Graph: convert every clause to two implications
- Find Strongly Connected Components: use Kosaraju’s or Tarjan’s algorithm.
- Check for Contradictions: if a variable and its negation are in the same SCC, the formula is unsatisfiable
Why SCC?
- SCCs are groups of nodes where every node is reachable from every other node.
- If a variable x and its negation ¬x are in the same SCC, the implications create a cycle of forced assignments that require x to be both True and False which implies unsatisfiable.
- If x and ¬x are in different SCCs, we can assign truth values in a topological order to satisfy all clauses.
Logic:
- If
xand¬xare in the same SCC,
→ contradiction ⇒ UNSATISFIABLE. - Otherwise, assign truth values by processing SCCs in reverse topological order:
- If
x’s SCC appears after¬x’s SCC → assignx = True - Else
x = False
Code : We will use Kosaraju’s algorithm for SCC finding.
struct TwoSAT {
int n; // number of variables
vector<vector<int>> g, gr; // graph and reverse graph
vector<int> comp, order, assignment;
vector<bool> used;
TwoSAT(int vars) {
n = vars;
g.assign(2 * n, {});
gr.assign(2 * n, {});
}
// get index of negation
int neg(int x) { return x ^ 1; }
// Add clause (a ∨ b)
// Equivalent to: (¬a → b) and (¬b → a)
void addClause(int a, int b) {
g[neg(a)].push_back(b);
g[neg(b)].push_back(a);
gr[b].push_back(neg(a));
gr[a].push_back(neg(b));
}
// First DFS (to get order)
void dfs1(int v) {
used[v] = true;
for (int to : g[v]){
if (!used[to]){
dfs1(to);
}
}
order.push_back(v);
}
// Second DFS (to assign components)
void dfs2(int v, int cl) {
comp[v] = cl;
for (int to : gr[v]){
if (comp[to] == -1){
dfs2(to, cl);
}
}
}
bool solve() {
int N = 2 * n;
used.assign(N, false);
comp.assign(N, -1);
// Fill order stack
for (int i = 0; i < N; i++){
if (!used[i]){
dfs1(i);
}
}
// Process in reverse order
reverse(order.begin(), order.end());
int j = 0;
for (int v : order){
if (comp[v] == -1){
dfs2(v, j++);
}
}
// Check for contradictions
assignment.assign(n, 0);
for (int i = 0; i < n; i++) {
if (comp[2 * i] == comp[2 * i + 1])
return false; // x and ¬x in same SCC → UNSAT
assignment[i] = comp[2 * i] > comp[2 * i + 1];
}
return true;
}
}4. Why do we care?
- Basic circuital design can be verified using 2-SAT
- Dependency resolution in software package installation is reduced to 2-SAT
- Type inference in programming languages can often be reduced to 2-SAT
Time Complexity: $O(m + n)$ due to SCC finding algorithm
Author – Suraj Kagalkar
Intresting reads
1st Read
A clear, high-level overview of 2-SAT: definitions, implication graphs, algorithms and applications.
Read More2nd Read
A compact, implementation-focused guide (implication graph + SCCs) with code and complexity notes
Read More3rd Read
“How to solve the 2-SAT problem in POLYNOMIAL TIME?”: A concise video walkthrough showing the implication-graph + SCC method step-by-step.
Read More4th Read
Algorithm for 2-satisfiability problem: Community Q&A with practical algorithmic tips, pitfalls, and implementation pointers from experienced coders.
Read MoreTask
Task #1
Checkout what 3-SAT problem is and why it is one of the hardest problems Checkout NP-hard, NP-complete problems.
